151121 初版 160204 更新
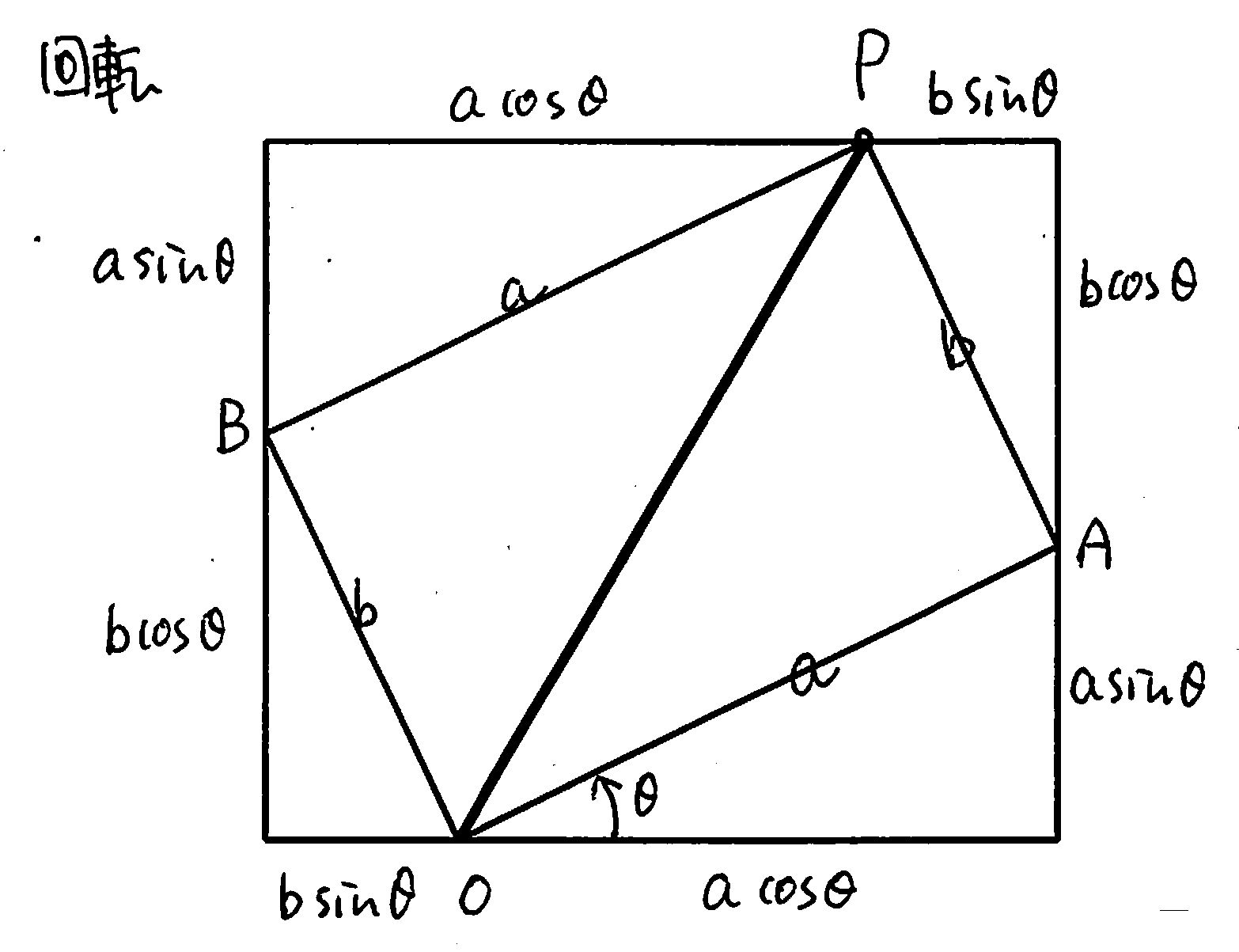
座標平面において,
点 (a, b) を原点中心に 角 θ だけ回転させた点を (x, y) とする。
\(\left\{
\begin{array}{l}
x = a\cos\theta-b\sin\theta\cr
y = a\sin\theta+b\cos\theta\cr
\end{array}\right.\)
行列を使って,記述すると
\(
\left(\begin{array}{c}
x\cr
y\cr
\end{array}\right)
=
\left(\begin{array}{cc}
\cos\theta & -\sin\theta\cr
\sin\theta & \cos\theta\cr
\end{array}\right)
\left(\begin{array}{c}
a\cr
b\cr
\end{array}\right)
\)
P(a, b) とする。
原点O との距離を r とする。
X(1,0) をとって,∠POX = α とする。
このとき,
(a, b) = (r cos α, r sin α) … ①
ところで,
x = r cos (α + θ) だから,
x = r cos α cos θ - r sin α sin θ
= a cos θ - b cos θ … ① より
また,
y = r sin (α + θ) だから,
y = r sin α cos θ + r cos α sin θ
= a sin θ + b cos θ … ① より