パラメータの入った二次関数の最大・最小 (2) 220208

\(k\) を定数とする。
\(f(x)=x^2-2kx+k+2\) について、
放物線\(y=f(x)\) の
軸の方程式は\(x=k\)
頂点の座標は\(\left(k, -k^2+k+2\right)\)
です。
区間\(0\leqq x\leqq 2\)…① における関数のとりうる値の範囲を考えてみましょう。

\(f(0)=k+2\) です。
\(f(2)=-3k+6\) です。
(i) 区間①で単調に増加していれば、 \(x=2\) で最大、 \(x=0\) で最小となります。
(ii) 区間①で単調に減少していれば、 \(x=0\) で最大、 \(x=2\) で最小となります。
(iii) 区間①に\(f(x)\) が極小となる\(x\) (すなわち\(k\)) が属していれば、 \(x=k\) で最小となり、 \(x=0\) または \(x=2\) で最大となります。 つまり、\(f(0)\) と \(f(2)\) の大きいほうが最大値です。

(1) 関数\(f(x)\) の最小値を \(k\) の式で表してください。
(2) 関数\(f(x)\) の最大値を \(k\) の式で表してください。

\(f(0)\), \(f(2)\), \(f(k)\) のグラフを同じ平面にかいてみよう。

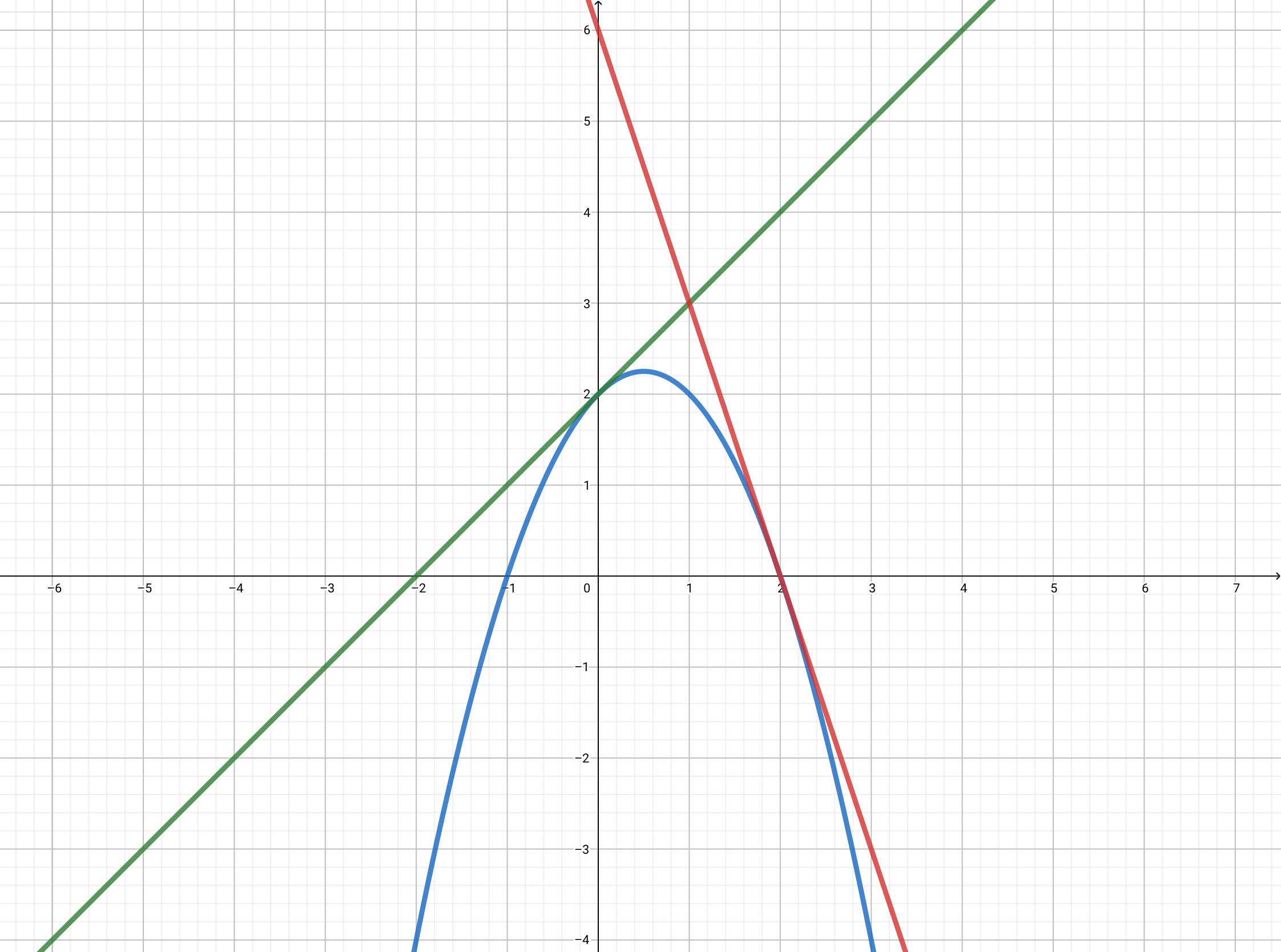
\(k=\dfrac{3}{2}\) のときの、\(y=f(x)\) (\(0\leqq x\leqq 2\)) のグラフ