東北大 2015 220217

問題
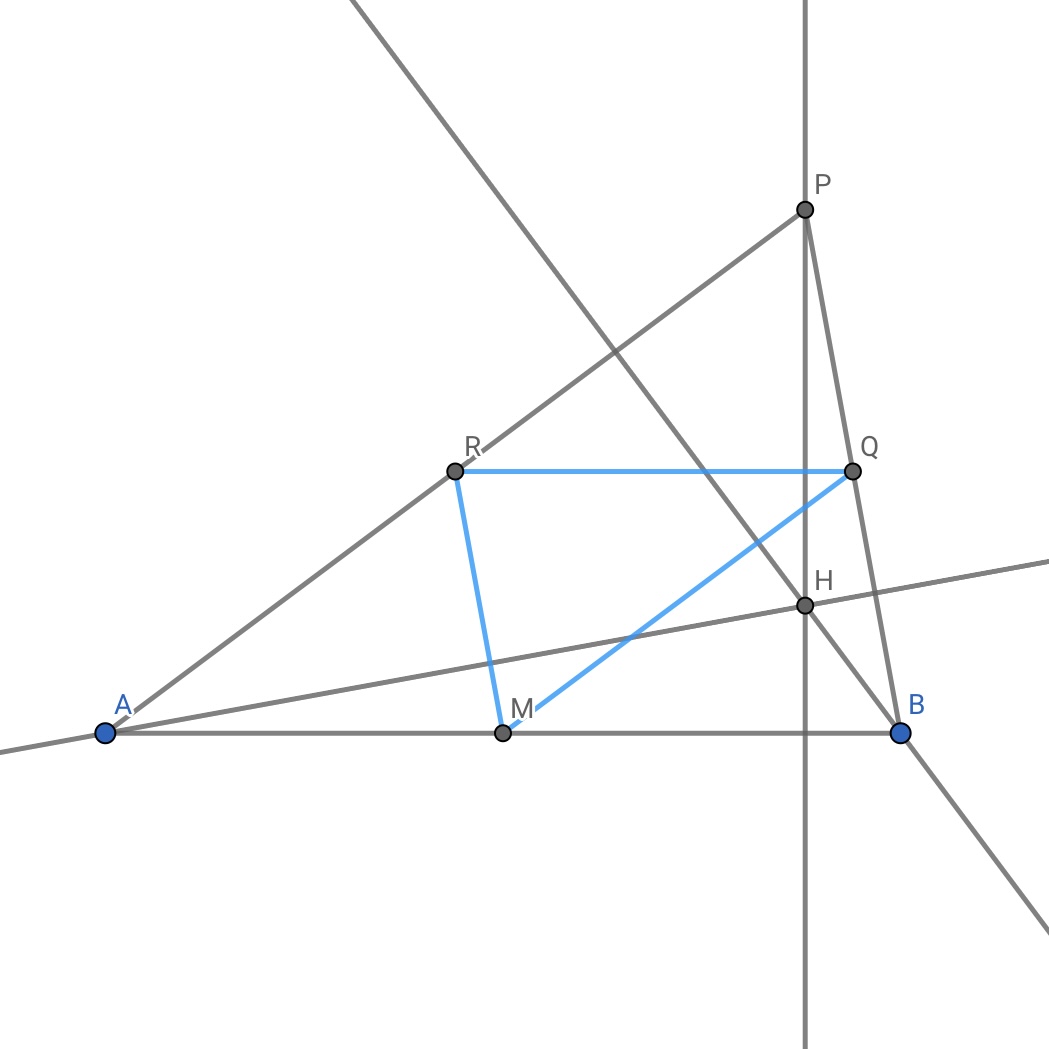
\(t> 0\) を実数とする。座標平面において、 3点 A\((-2,0)\), B\((2,0)\), P\((t,\sqrt{t})\) を頂点とする三角形 ABP を考える。
(1) 三角形 ABP が鋭角三角形となるような \(t\) の範囲を求めよ。
(2) 三角形 ABP の垂心の座標を求めよ。
(3) 辺 AB, Bp, PA の中点をそれぞれ M, Q, R とおく。 \(t\) が (1) で求めた範囲を動くとき、三角形 ABP を線分 MQ, QR, RM で折り曲げてできる四面体の体積の最大値と、そのときの \(t\) の値を求めよ。

例えば、点 P の動きを考えてみましょう。
P を通り、直線 QR に垂直な平面を α₁ とします。　
直線QR と α₁ との交点を S₁ とします。
P は α₁ 上で、中心 S₁, 半径 PS₁ (\(r_1\) とおきます) の円を描きます。
GeoGebra 3d では、QR を軸にして、Pを通る円をかかせればいいです。
動画(geogebra.org へのリンク)のように同期させて動かしたいので、工夫を考えます。
円は直線 QR に垂直な平面上にあるので、 P から \(xy\) 平面へ下した垂線の足 (点 P の \(xy\) 平面への射影ということにします。) は RQ に垂直な直線上にあります。
RQ と AB は平行ですから、この直線は P を通り、辺 AB に垂直です。
同様なことが、A, B についてもいえますので、 A, B, P が重なった点を C とすると、C の \(xy\) 平面への射影 H は、三角形ABP の垂心になります。

点 P の軌跡を考えるのは、座標の設定から比較的簡単です。
点 A の軌跡について、もう少し具体的に考えてみます。
MR を軸にして、A を回転させた円を考えます。
中心を S₂ とすると、S₂ は RM と AH の交点です。
半径 \(r_2\) は線分 AS₂ ですが、この大きさは三角形 AMR の MR を底辺とした高さに等しいです。つまり、三角形 ABP の BP を底辺とした高さの半分です。
A を角 θ だけ回転した点を A' とします。
このとき、\(\overrightarrow{\rm S_2A^\prime}\) \(=(\cos\theta)\overrightarrow{\rm S_2A}\) \(+(0,0,r_2\sin\theta)\) と表すことができます。
\(\overrightarrow{\rm S_2A}\) については、大きさは\(r_2\)です。平面のおける直線 MR (BP でもよい)の法線ベクトルと平行です。ベクトルは便利です。

三角形 MQR を底面と見たときの、四面体の高さは CH です。
H の座標は計算することができます。 C の \(x\), \(y\) 座標がわかったことになります。
直角三角形 CS₁H に注目すると、 CS₁, S₁H は比較的簡単に計算できますから、 CH の長さを求めることができます。
直角三角形 CS₂H に注目します。 \(\angle{\rm CS_2H}=\theta_2\) とおくと、 \(\sin\theta_2=\dfrac{\rm CH}{r_2}\) です。 A から C までは \(\theta_2\) だけ回転すればよいことがわかります。鋭角か鈍角のどちらかは考察する必要があります。