余弦定理と二次方程式の解 220221

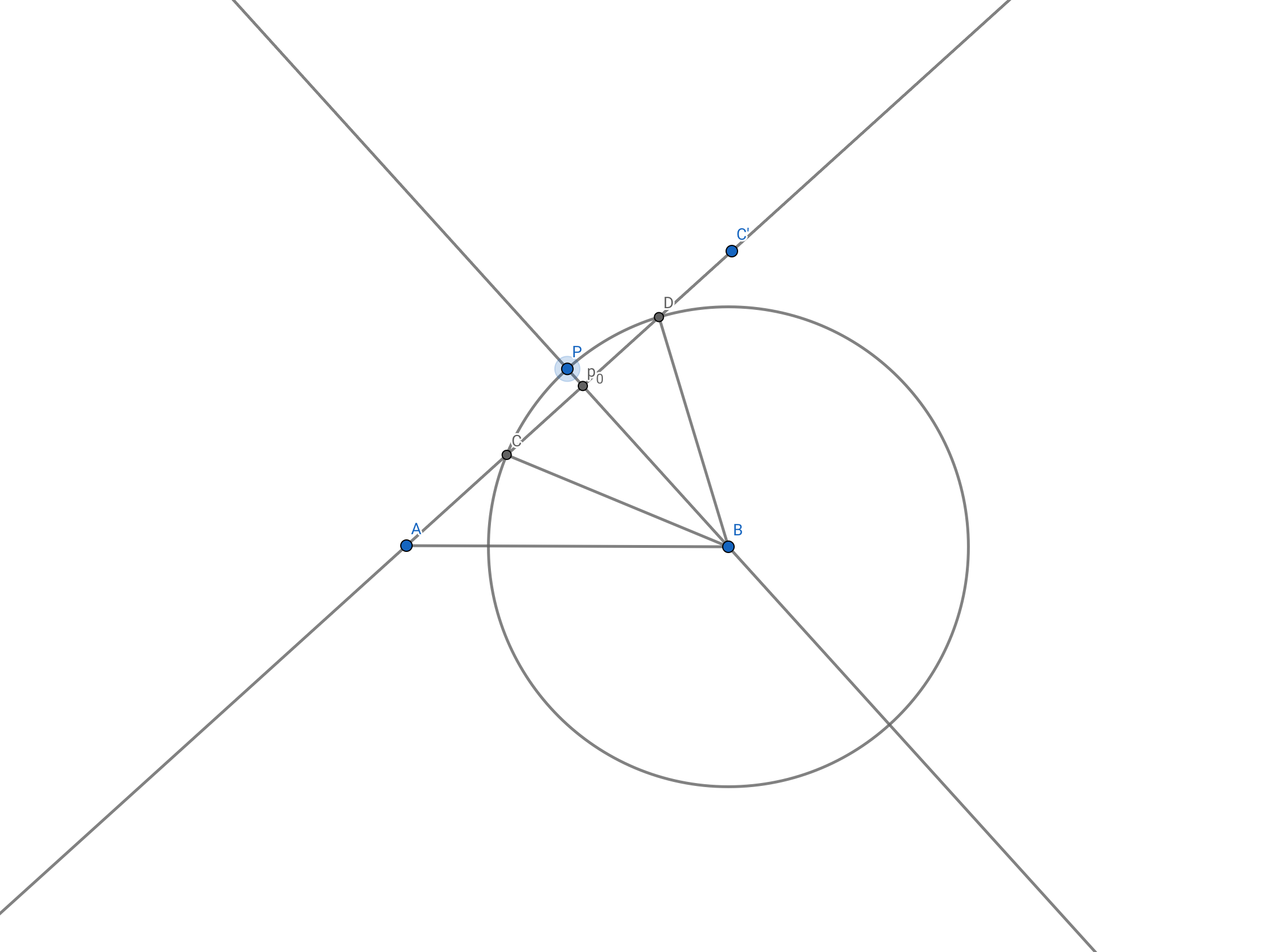
図において、AB の長さを c として固定します。
角 BAC' の大きさを固定します。こちらを単に角 A とします。
B から直線 AC' (ℓ とします) に下した垂線の足が P₀ です。
BP₀ の長さを h とすると、 \(h=c\sin A\) で c, A を一定にしているので、h も一定です。
直線 BP₀ 上に点 P をとります。
点 B を中心に P を通る円を考えます。 \({\rm BP}=a\) として、P を動かします。 つまり、a の値、円の半径を変化させます。 a と 直線 BC' の共有点について調べます。 共有点は最大で2個です。

いま、共有点が A より P₀ 側に異なる２つあるときを考えます。 C, D とします。 AC を α, AD を β とします。
図より h< a < c のときです。
式ではどのように表現されるでしょうか。
余弦定理より、α, β は 次の x についての二次方程式の実数解です。
\(a^2=x^2+c^2-2cx\cos A\)
直角三角形 ABP₀に注目して、\(c\cos A={\rm AP_0}\) です。 これを b₀ とおくことにすると、
\(x^2-2b_0x+c^2-a^2=0\)…①
二次方程式① の判別式 D は、 \(D=4({b_0}^2+a^2-c^2)\)
直角三角形 ABP₀ において、ピタゴラスの三平方の定理から、 \(h^2+{b_0}^2=c^2\)
したがって、\(D=4(a^2-h^2)\)
式からも、方程式 ① は 0 < h < a < c のときに、異なる2つの正の解をもつことがわかります。
方程式の解は \(b_0+\sqrt{a^2-h^2}\), \(b_0-\sqrt{a^2-h^2}\) です。
図によるイメージと一致しています。
また、 a < h ならば、円と直線 AC' は共有点をもちません。
a = h のときは、直線 ℓ は 円の接線になります。 方程式① は重解 b₀ をもちます。

h < c < a のときはどうでしょうか。
方程式① は異なる2つの実数解をもちますが、 1つは負の値になります。
図において \({\rm AD}=b_0+\sqrt{a^2-h^2}\),  \(-{\rm AC}=b_0-\sqrt{a^2-h^2}\) です。
AC の長さは、
\(a^2=x^2+c^2-2cx\cos \angle{\rm BAC}\) …② の正の解ですが、 ∠BAC = \(\pi\) - A ですから、
② は \(x^2+2b_0x+c^2-a^2=0\) となります。