大阪大 2015 220222

YouTube みんなでGeoGebra 円と2点を共有して内部にある三角形の面積

問題
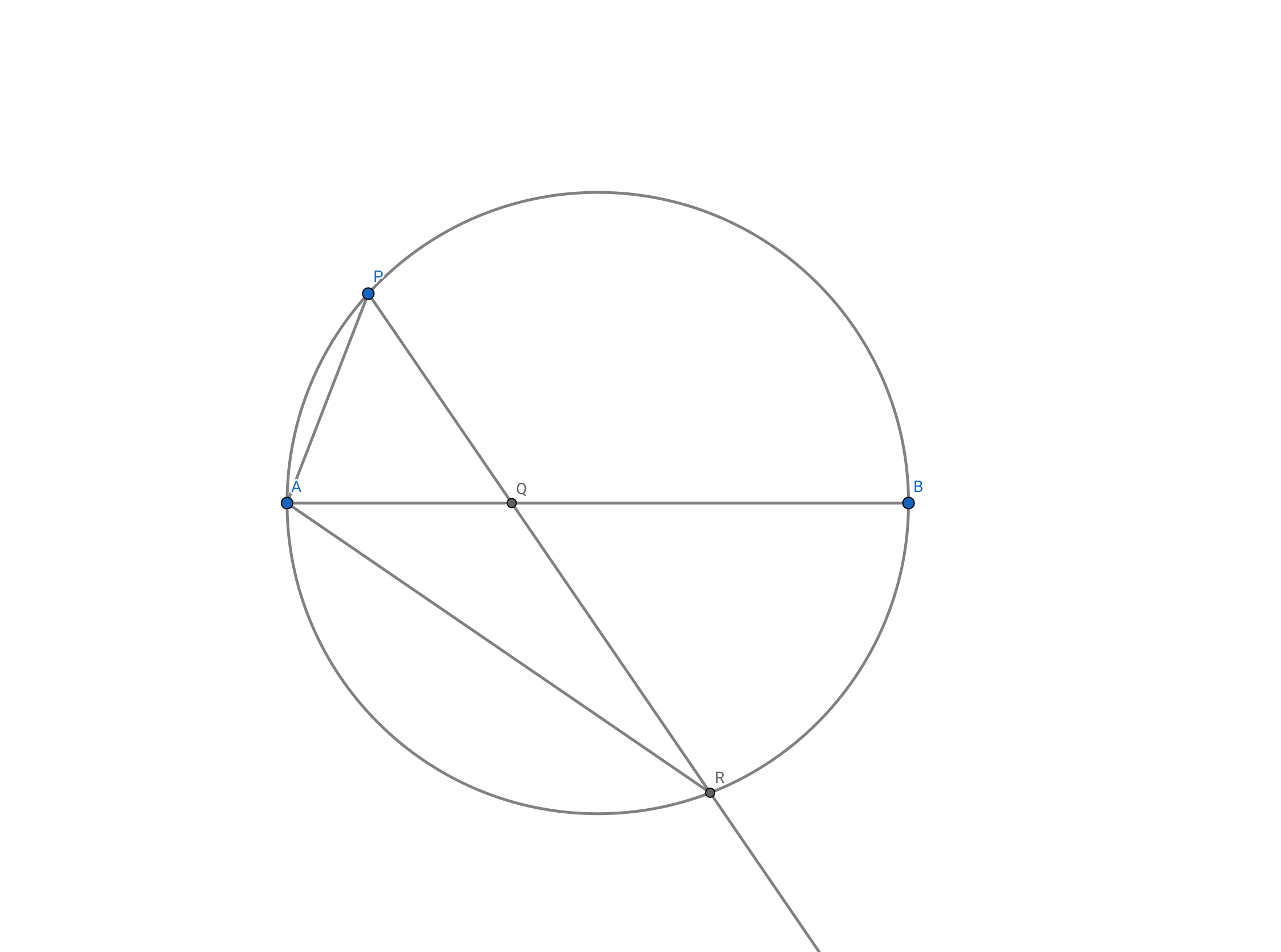
平面上に長さ 2 の線分 AB を直径とする円 C がある。 2点 A, B を除く C 上の点 P に対し、 AP = AQ となるように線分 AB 上の点 Q をとる。 また、直線 PQ と 円 C の交点のうち、 P でない方を R とする。
(1) △AQR の面積を \(\theta=\angle{\rm PAB}\) を用いて表せ。
(2) 点 P を動かして△AQR の面積が最大になるとき、 \(\overrightarrow{\rm AR}\) を \(\overrightarrow{\rm AB}\) と \(\overrightarrow{\rm AP}\) を用いて表せ。